
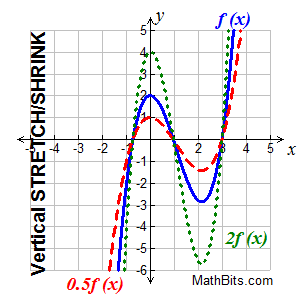
If \(0 If \(0 1\), then the graph will be compressed by \(1/b\). Reflect > Shift > Stretch Inside parentheses think opposite for stretches and shifts and FACTOR (if necessary) Inside parentheses horizontal changes.If \(a > 1\), then the graph will be stretched.This results in the graph being pulled outward but retaining the input values (or x). you will see that the graph has been stretched vertically by a factor of 2 and shifted. Vertical stretch occurs when a base graph is multiplied by a certain factor that is greater than 1. If the constant is greater than 1, we get a vertical stretch if the constant is between 0 and 1. Given a function \(f(x)\), a new function \(g(x) = a f(x)\), where \(a\) is a constant, is a vertical stretch or a vertical compression of the function \(f(x)\). The graph of a function is reflected about the y -axis if each x. Horizontal And Vertical Graph Stretches And Compressions (Part 1) y c f(x), vertical stretch, factor of c y (1/c)f(x), compress vertically, factor of c y. When we multiply a function by a positive constant, we get a function whose graph is stretched vertically away from or compressed vertically toward the x-axis in relation to the graph of the original function. The graph of an absolute value function yx-1-1 can be reflected in the x-axis by. The graph of an odd function is symmetric about the origin. The graph of a function can be vertically stretched or shrunk by. A function called an odd function if for every input \(x\) \(f(x)= -f(-x)\). The graph of an even function is symmetric about the y-axis. Even and Odd Functions (Symmetry)Ī function is called an even function if for every input \(x\) \(f(x) = f( -x)\). Given a function \(f(x)\), a new function \(g(x) = f(-x)\) is a horizontal reflection of the function \(f(x)\) over the y-axis.įigure 3 You will see the horizontal and vertical reflection of a function \(f(x)\). Given a function \(f(x)\), a new function \(g(x) = - f(x)\) is a vertical reflection of the function \(f(x)\) over the x-axis. When \(k\) is negative, then the graph will translate \(k\) units downward on the y-axis.įigure 2 There is Vertical Shift of the function \(f(x) = ∛x\) thus \(k = 1\). When \(k\) is positive, then the graph will translate \(k\) units upward on the y- axis. Stretching f(x) vertically by a factor of 3 will result to h(x) being equal to 3 times f(x). A quadratic equation is an equation of the form y ax2 + bx + c, where a, b and c are constants. Given the function \(f(x)\), a new function \(g(x) = f(x) + k\), where \(k\) is a constant of the function \(f(x)\). Ordinate The y-coordinate Shift A translation in which the size and shape of a graph of a function is not changed, but the location of the graph is. When \(h\) is positive, then the graph \(y = f(x)\) will translate h units to the right of the x- axis.When \(h\) is negative, then the graph \(y = f(x)\) will translate \(h\) units to the left of the x-axis.įigure 1 There is Horizontal Shift of the function \(f(x) = ∛x\) thus \(h = +1\) Note: that the function is shifting left after the addition of 1. Definition: Vertical Shift Given a function f(x), a new function g(x) f(x) + k, where k is a constant, is a vertical shift of the function f(x). Given a function \(f\), a new function \(g(x) = f(x – h)\), where \(h\) is a constant of the function \(f\). The transformations vary as follows: Horizontal Translation Combine transformations to make a new graph.įor a function \(y = f(x)\), the general equation \(y = a f(x - h) + k\) is a transformation if \(a, h,\) and \(k\) are real numbers with \(a ≠ 0\). 1 (c) Absolute Value Function (d) Square Root Function f(x) x2 3 33 1 f(x) x3 2 332 (e) Quadratic Function Figure 1.Graph functions using compressions and stretches.Graph functions using reflection about the x-axis and y-axis.

Graph functions using reflections about the x-axis and the y-axis.


 0 kommentar(er)
0 kommentar(er)
